Definición
La función exponencial de base con y , con posee una inversa que se denomina función logarítmica de base . Esta función es tal que .
Puesto que estas funciones son inversa una de la otra entonces si y solo si . Por ejemplo, puesto que , entonces .
Propiedades
Por la razón anterior, de las propiedades de la exponencial se deducen propiedades correspondientes de la logarítmica, tales como las que se consignan en la siguiente tabla.
| Propiedad de la exponencial base | propiedad correspondiente de la logarítmica |
|---|---|
Otra propiedad importante de los logaritmos es que si y son números reales positivos y diferentes de 1, entonces
Ecuaciones
Puesto que la función logarítmica es inyectiva, entonces de la igualdad se obtiene que . Esto permite resolver algunas ecuaciones que involucran logaritmos.
Por ejemplo, determinar para qué valor o valores de se cumple que .
El lado izquierdo de la ecuación es igual a , por lo que . Por lo tanto , es decir y, de aquí, , . Puesto que el logaritmo está definido para números reales positivos, no está definido. Por otra parte, si se sustituye por en la ecuación se obtiene una proposición verdadera. Solo satisface la ecuación.
Gráfica
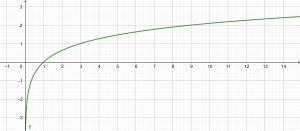
Si a > 1 entonces la función logarítmica g : ℝ+ → ℝ con g(x) = logax es creciente. Su gráfica es:
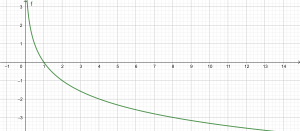
Si 0 < a < 1 entonces la función logarítmica g : ℝ+ → ℝ con g(x) = logax es decreciente. Su gráfica es: