|
Aquí encontrará un conjunto de conceptos relacionados con el tema de estudio. Solamente debe dar clic en la pestaña para desplegar el contenido. |
Centro y razón k de homotecia
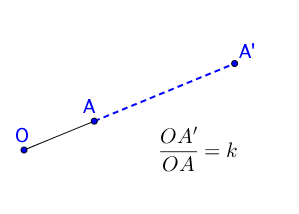
En una homotecia se hace corresponder a un punto A otro A’, alineado con A y con otro punto fijo O, tal que: OA’/OA= k, siendo k = 0 . Al punto O se le denomina centro de homotecia, y al número k razón de la homotecia.
Homotecia directa
En una homotecia directa la razón de homotecia (𝑘) es mayor que cero (𝑘 > 0), asimismo se da la relación 𝑂 − 𝐴 − 𝐴′ ó 𝑂 − 𝐴′ − 𝐴 donde 𝑂 es el centro de la homotecia y 𝐴′ es el punto homólogo de 𝐴, a esta relación se le llama homotecia positiva. Específicamente cuando 0 < 𝑘 < 1 se dice que la figura sufre una disminución o contracción, cuando 𝑘 = 1 se le llama identidad, cuando 𝑘 > 1 se dice que la figura sufre una ampliación o dilatación.
|
Ampliación o dilatación (k > 1) |
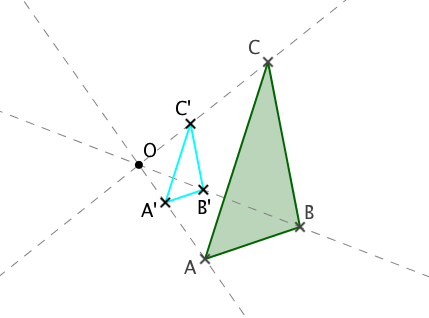
Disminución o contracción (0< k < 1) |
 |
 |
|
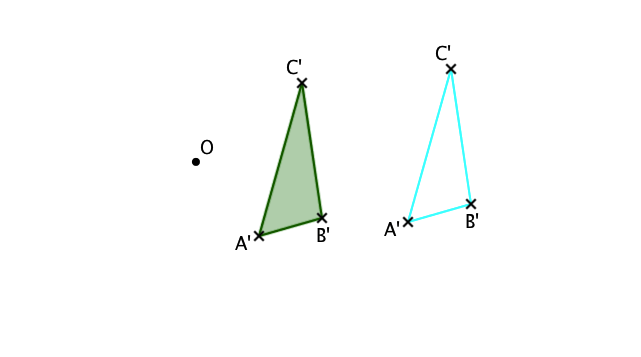
Identidad (k = 1) |
|
 |
|
Homotecia indirecta o inversa
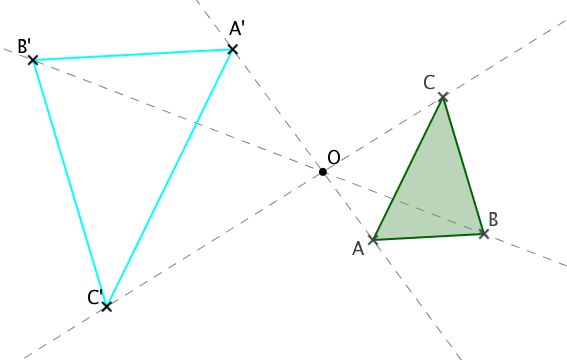
Se da cuando la razón de homotecia (𝑘) es menor que cero (𝑘 < 0), ocurre la relación 𝐴′ − 𝑂 − 𝐴 ó 𝐴 − 𝑂 − 𝐴′, donde 𝑂 es el centro de la homotecia y 𝐴′ es el punto homólogo de 𝐴, a esta relación se le llama homotecia negativa. Particularmente cuando −1 < 𝑘 < 0 se dice que la figura sufre una disminución o contracción, cuando 𝑘 = −1 se le llama simetría central, cuando 𝑘 < −1 se dice que la figura sufre una ampliación o dilatación.
|
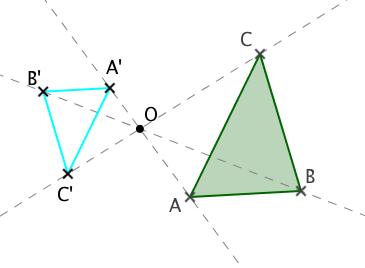
Disminución o contracción (−1 < k < 0) |
Ampliación o dilatación (k < -1) |
 |
 |
|
Simetría central (k = -1 ) |
|
Trasformación geométrica
Una transformación en el plano es una correspondencia uno a uno del conjunto de puntos del plano en sí mismo. En una trasformación geométrica hay que tener en cuenta:
- la figura original
- una regla u operación que describa el cambio, y
- la figura que resulta después del cambio.