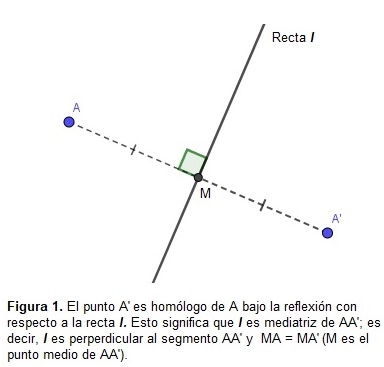
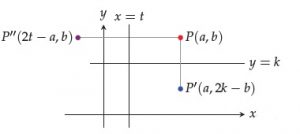
Una reflexión en el plano con respecto a una recta l, es una transformación tal que cada punto A, asigna un punto A’ (llamado homólogo de A) tal que l es perpendicular en su punto medio (M) al segmento AA’. Una reflexión es una isometría, es decir, conserva las distancias y las medidas de los ángulos.
A continuación se muestran dos ejemplos, en la Figura 1. Puntos homólogos respecto a la recta l.
En la Figura 2. Imágenes idénticas que se reflejan respecto al eje Y.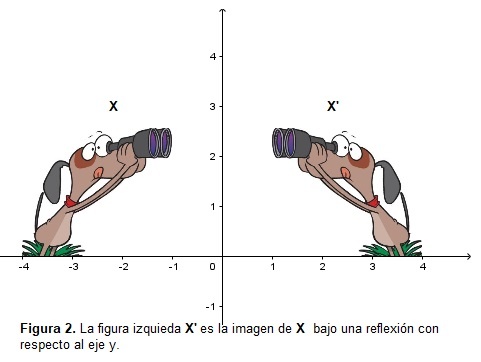
Imagen de un polígono
Si se considera el polígono de vértices A (2,2), B (1,5), C (5,4), D (4,1) y E (3,3). Se puede determinar su homólogo bajo la reflexión con respecto al eje y. Entonces, el homólogo de (x, y) bajo la reflexión con respecto al eje x es (–x, y). De esta manera:
| A(2,2) = A’( – 2, 2)
B(1,5) = B’( – 1, 5) C(5,4) = C’( – 5, 4) D(4,1) = D’( – 4, 1) E(3,3) = E’( – 3, 3) |
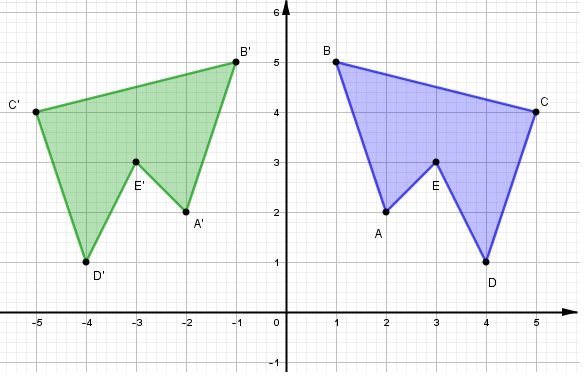 |
Al representar los polígonos en un sistema de coordenadas, se tiene que el polígono verde es homólogo al polígono azul con respecto al eje y. Como se muestra en la figura de la derecha.
Cálculo de un punto homólogo
Si se desea determinar el punto homólogo de B, es necesario trazar la recta perpendicular a y = -x + 3 que contiene al punto ( -2 , 0 ).
 |
Se debe determinar el punto de intersección entre las rectas y establecer la distancia entre el punto B y la recta, para establecer dónde ubicar el punto homólogo.
Se utiliza el punto de intersección de las rectas que son perpendiculares como centro y la distancia del cento al punto B, como radio. |
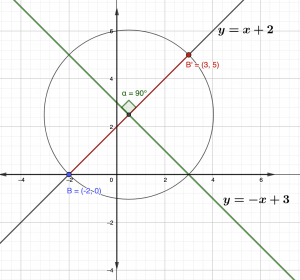 |
Después de trazar la circunferencia con esos valores, se logrará determinar el homólogo de B. Observe como B’ es el otro punto que interseca la recta perpendicular con la circunferencia.
Los dos puntos de intersección de la circunferencia con la recta que contiene a B son homólogos entre sí.
En la imagen se ha trazado la recta perpendicular a y = -x + 3 y que contiene el punto (-2 , 0), que corresponde a y = x + 2. Para ampliar el tema se puede acceder a https://recursoslibres.reformamatematica.net/funcion-lineal-desarrollo-tema/.
|