 |
A continuación se presentan las habilidades específicas vinculadas con el problema "¿Cuál función es más acorde?" y otros elementos didácticos pertinentes. |
Habilidades específicas que se trabajan con el problema
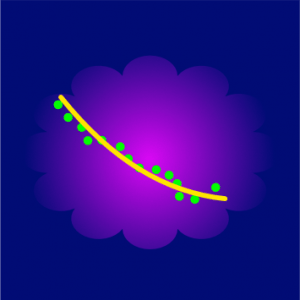
Después de trabajar las diferentes tipos de funciones de acuerdo a su criterio, es decir, las funciones lineales, cuadráticas, exponenciales, logarítmicas y la raíz cuadrada; es importante conocer cuales fenómenos pueden ser representados con estas funciones. Precisamente esto es lo que se busca en el problema de esta Unidad Virtual de Aprendizaje. Dicho problema se refiere a la habilidad específica:
- Analizar el tipo de función que sirva de modelo para una situación dada. (MEP, 2012, p.417)
Es importante diferenciar esta habilidad a la de otras que hacen referencia al uso de modelos matemáticos, como por ejemplo las habilidades 14 (de décimo año), 8 y 14 (de undécimo año).
Indicaciones metodológicas
El problema "¿Cuál función se ajusta mejor?"se puede aprovechar en diferentes aspectos de acuerdo al Programa de Estudios de Matemática de Costa Rica (alguna terminología empleada a continuación es propia del currículo nacional)
- Este es un problema que se puede trabajar en la Etapa I (Aprendizaje de los conocimientos), ya que en décimo y undécimo se han trabajado las diferentes funciones y su aplicación en diferentes modelos. Por cuestión de tiempo, se podría dar sólo una (de las tres) informaciones dadas en el problema a cada subgrupo.
- En el tercer momento donde los estudiantes exponen sus ideas, se les indica que hay diferentes problemas, por lo que la solución o modelo matemático encontrado en uno de los grupo, no necesariamente coinciden.
- Para la clausura es importante hacer referencia a elementos particulares de cada tipo de función, para comparar dichas funciones. Por ejemplo, el "crecimiento rápido" de una función exponencial creciente, o el "crecimiento lento" de una función logarítmica creciente.
- Otro elemento importante a tratar en la clausura es la "inexactitud" de los modelos matemáticos, haciendo referencia a que son aproximaciones a una situación de la vida cotidiana, y que a pesar de que existan funciones que modelizan ciertas situaciones, algunos elementos (preimagen e imagen) no necesariamente cumplen dicha función, sino que es una aproximación muy cercana a la realidad. Esta idea se refuerza en el video 3 de Desarrollo de tema (utilizando la representación gráfica) y en el video 4 de Desarrollo del tema (utilizando la representación algebraica)
- Además, se debe explicar el rol del dominio de la función que modeliza una situación, pues normalmente tiene un dominio muy restringido, y fuera de este dominio los valores no tienen sentido en el contexto. En el video 2 de Desarrollo del tema se analiza esto en el caso del problema de las semana de gestación del feto.
- En el caso de secundaria, el único modelo algebraico que se puede construir es el lineal, ya que con las habilidades sobre el cálculo de la pendiente y ordenada, tal y como se muestra en el video 4 de Desarrollo del tema, se puede calcular un modelo lineal utilizando un par de puntos. Aquí es importante insistir (tal y como se dice en el video) que esta función que se estaría averiguando no es la de mejor ajuste. Para lograr lo anterior, es necesario algún tipo de software, tal y como se muestra en el video 5 de Desarrollo del tema.
- Los conceptos de interpolación y extrapolación descritos en el video 3 de Desarrollo del Tema, son fundamentales, principalmente para que los estudiantes comprendan que cuando se esta extrapolando, el modelo encontrado puede que no tenga sentido en la realidad. Se pueden aprovechar los otros dos problemas para reforzar estas ideas matemáticas.
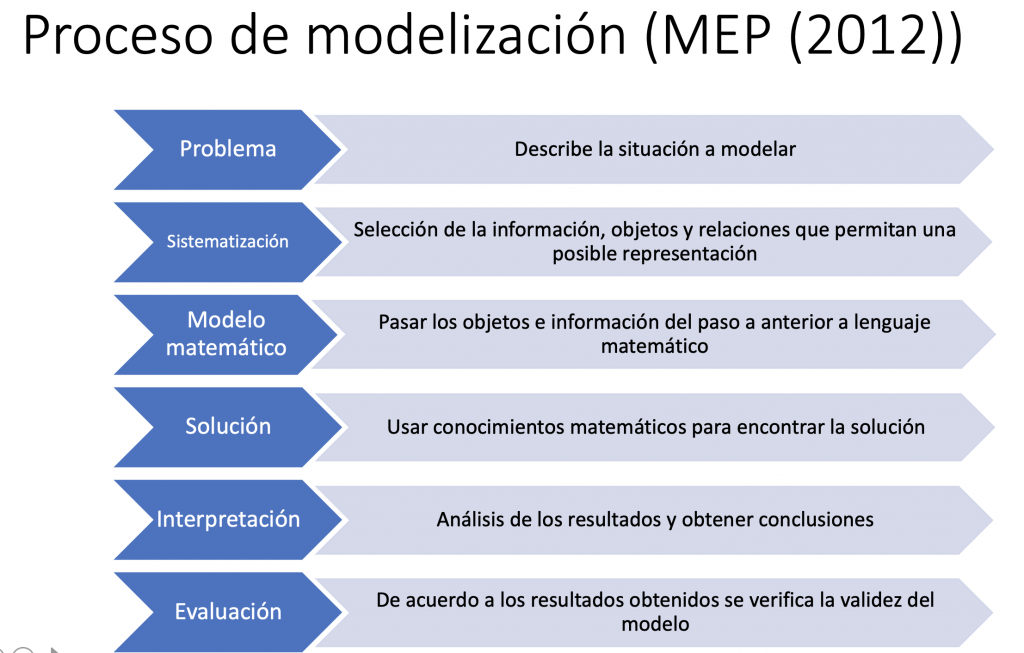
- De acuerdo a los Programa de Estudios de Matemática de Costa Rica, , el proceso para llevar a cabo la modelización se resumen en 6 pasos:
Nivel de complejidad y procesos matemáticos
El nivel de complejidad del problema "¿Cuál función es ajusta mejor?" es de reflexión según la solución presentada en el video y la intervención de los procesos matemáticos que se describen a continuación:
Razonar y Argumentar:
Este proceso se activa a un nivel alto, ya que el estudiante debe tener claro los conceptos de cada tipo de función, sus características y limitaciones, para poder relacionarla con cada uno de los modelos presentados.
Plantear y resolver y problemas:
Este proceso se activa a un nivel alto, pues es necesario trasladar la información dada a alguna otra representación para evaluar y compararlo con los conocimientos previos sobre las funciones. En el caso de la modelización, cada problema es un reto nuevo para el estudiante.
Conectar:
La conexión entre conceptos como representaciones de una función, imágenes, preimágenes, características de una función, entre otros, para resolver problemas de contexto real, hace que este proceso se activa a nivel alto.
Comunicar:
Posterior al análisis que se realizó, la solución de este problema se da en forma natural, pues debe decidir cuál es la función que mejor se ajusta en cada caso, por esta razón este proceso se activa a nivel intermedio.
Representar:
Se utiliza la representación tabular (dada) para construir la representación gráfica (no dada) pues de esta forma se visualiza mejor el comportamiento de los datos del problema. En este caso se utilizan dos representaciones. Por esta razón este proceso se activa a nivel intermedio.
Por tanto, tres de los procesos matemáticos alcancan una intervención alta. El nivel de complejidad del problema es de análisis, debido a las exigencias cognitivas que implica para el estudiante y que fueron detalladas previamente. Se puede profundizar en la estrategia para determinar los niveles de complejidad en Ruiz (2018). Además puede acceder a los videos de la colección Valoración de Tareas Matemáticas para ampliar los contenidos.
Profundizando en la modelización
En este video se profundiza en el uso de la modelización en problemas no funcionales.


