 |
A continuación, se presentan las habilidades específicas vinculadas con el problema desarrollado y otros elementos didácticos referidos al tema. |
Habilidades específicas que se trabajan con el problema
A través del problema Tornillos hexagonales se trabajó un tema que pertenece a Polígonos, de décimo año, incluye el estudio lado, radio, apotema, ángulo central, ángulo interno, ángulo externo, diagonal y relaciones métricas.
En general este tema incluye las siguientes habilidades específicas:
12. Determinar las medidas de los ángulos internos y externos de polígonos en diferentes contextos (MEP, 2012, p. 389).
13. Determinar la medida de la apotema y el radio de polígonos regulares y aplicarlo en diferentes contextos (MEP, 2012, p. 389).
Indicaciones metodológicas
Respecto a la organización de la lecciones, el MEP (2012, pp. 41-44) establece dos etapas, el problema Tornillos hexagonales puede ser empleado en la I Etapa: El aprendizaje del conocimiento, debido a que los estudiantes poseen los conocimientos previos para enfrentar el reto. Es importante resaltar que la solución, la discusión interactiva y comunicativa le ofrecerán los recursos para formalizar la información vinculada con las habilidades específicas 12 y 13, en particular las fórmulas relacionadas con el cálculo ángulos y la longitud del lado, radio y apotema.
Nivel de complejidad y procesos matemáticos
El nivel de complejidad del problema Tornillos hexagonales es de Reproducción, esto se asocia con la solución presentada y la intervención de los procesos matemáticos que se describen a continuación:
Este proceso se activa de manera intermedia, debido primeramente a que la información matemática no está dada de manera explícita en el enunciado, aunque las longitudes se conocen, para responder a la pregunta ¿Se puede concluir que la cabeza del tornillo es un hexágono regular?, se requiere de un conjunto de calculos preliminares para determinar si el polígono es convexo, además, si sus lados y ángulos son congruentes.
Plantear y resolver problemas:
El problema se puede considerar familiar para el estudiante. Además, requiere de emplear algoritmos conocidos como las razones trigonométricas y resolución de ecuaciones, por tanto, la intervención del proceso es baja.
Conectar:
En la solución los estudiantes deben conectar y usar oportunamente la información que les proporciona el contexto del problema (información sobre el tornillo) con los conocimientos involucrados: radio, apotema y la razón trigonométrica coseno. En este sentido la intervención del proceso se puede catalogar como intermedia.
Comunicar:
En este problema el estudiante debe emitir una conclusión a través de lenguaje natural y esto debe permitir exponer sus acciones, razonamientos y resultados, por tanto, esto implica una participación intermedia de este proceso.
Representar:
La intervención del proceso es intermedia, debido a que los estudiantes deben interpretar la información dada de manera gráfica cuando se enfrentan a esto: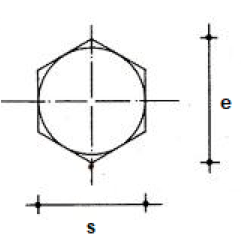
Además, recibe información mediante una representación tabular:
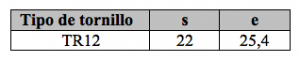
Finalmente, debe usar los datos recibidos y transformarlos a una representación algebraica como lo es la ecuación que surge de la razón trigonométrica, esto implica interpretar, razonar y trasformar la información codificada que esta presente en el problema.
Por tanto, cuatro de los procesos matemáticos alcanzan una intervención intermedia. El nivel de complejidad del problema es de Conexión, debido a las exigencias cognitivas que implica para el estudiante y que fueron detalladas previamente. Se puede profundizar en la estrategia para determinar los niveles de complejidad en Ruiz (2018). Además puede acceder a los videos de la colección Valoración de Tareas Matemáticas para ampliar los contenidos.