|
A continuación se presentan las habilidades específicas vinculadas con el problema desarrollado y otros elementos didácticos referidos al tema. |
Habilidades específicas que se trabajan en el problema
El tema de visualización espacial, en décimo año incluye el estudio de la esfera, su radio, diámetro y sección plana, mediante las siguientes habilidades específicas:
18. Identificar el radio y el diámetro de una esfera (MEP, 2012, p. 392)
20. Determinar qué figuras se obtienen mediante secciones planas de una esfera o un cilindro y características métricas de ellas (MEP, 2012, p. 393).
Indicaciones metodológicas
El problema Circunferencia de la Tierra esta diseñado para la I Etapa: Aprendizaje del conocimiento (MEP, 2012, p. 41-44) , debido a que se deben emplear conocimientos previos sobre la circunferencia y razones trigonométricas, para determinar el dato faltante. Y a través del procesos de resolución del problema se pueden formalizar las secciones planas de la esfera y algunas de sus relaciones métricas.
De acuerdo con la MEP (2012, p. 401) se deben tener los siguiente aspectos en consideración:
- En cuanto al estudio de las esferas, se busca la identificación de sus elementos, y además, identificar las figuras que se forman cuando se cortan con un plano. Para esto pueden ayudar modelos con plastilina, u otro material que pueden ser cortados para evidenciar qué sección plana contiene.
- El uso de de software de geometría dinámica junto con material concreto(plastilina, arcilla moldeable, esferas de estereofón, entre otros) facilita la visualización. Además, deberá evaluarse la determinación de figuras mediante secciones planas y las relaciones métricas entre ellas.
Niveles de complejidad y procesos matemáticos
El nivel de complejidad del problema Circunferencia de la Tierra es de Conexión, esto se asocia con la solución presentada y la intervención de los procesos matemáticos que se describen a continuación:
Razonar y Argumentar:
Este proceso se activa en un nivel intermedio, debido a que la respuesta se obtiene únicamente después de haber realizado el tratamiento matemático de la información brindada, aplicar la razón trigonométrica seno y despejar la variable r. Posteriormente, se debe emplear el dato hallado (el radio) en la fórmula de la circunferencia, para dar respuesta al cuestionamiento planteado.
Plantear y resolver problemas:
El problema se puede considerar familiar para el estudiante. Además, requiere de emplear algoritmos conocidos la razón trigonométrica seno y el despeje de una ecuación, por tanto, la intervención del proceso se puede catalogar como baja.
Conectar:
En la solución los estudiantes deben conectar oportunamente la información que les proporciona el contexto del problema y los conceptos involucrados (radio, hipotenusa, seno, ángulo y altitud). Esta es una situación que resulta familiar y similar a las estudiadas previamente. En este sentido la intervención del proceso se puede catalogar como baja.
Comunicar:
Los estudiantes deben interpretar y seguir una secuencia de razonamientos matemáticos, donde usan los conceptos y procedimientos, lo anterior lo deben expresar de manera escrita para poder terminar la respuesta, por tanto, esto implica una intervención intermedia del proceso. Un ejemplo de esto es la siguiente secuencia: usar la información dada de manera literal, hacer una representación gráfica de la situación, escribir una ecuación que modele la situación y plasmar una respuesta “la circunferencia es de aproximadamente 39890, 88 km”.
Representar:
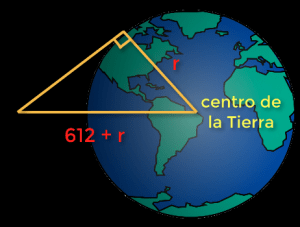
La intervención del proceso es intermedia, debido a que los estudiantes deben interpretar la información dada de manera literal por ejemplo “gira entorno a la tierra a una altitud de 612 km” y transformarla en una representación gráfica como el triángulo rectángulo que se forma, observe la siguiente imagen:
Además, se emplea una representación algebraica, la ecuación que permite determinar el radio de la esfera, esto implica interpretar, razonar y transformar la información codificada que esta presente en el problema.
Por tanto, tres de los procesos matemáticos alcanzan una intervención intermedia. El nivel de complejidad del problema es de Conexión, debido a las exigencias cognitivas que implica para el estudiante y que fueron detalladas previamente. Se puede profundizar en la estrategia para determinar los niveles de complejidad en Ruiz (2018). Además puede acceder a los videos de la colección Valoración de Tareas Matemáticas para ampliar los contenidos.