|
A continuación se presentan las habilidades específicas vinculadas con el problema desarrollado y la aproximación de áreas, así como otros elementos didácticos pertinentes. |
A continuación se presentan las habilidades específicas vinculadas con el problema desarrollado y la "Aproximación de áreas", así como otros elementos didácticos pertinentes.
Habilidades específicas que se trabajan con el problema
A través del problema Zacate para el jardín se trabajó un tema que pertenece a Polígonos, de décimo año, incluye el estudio perímetros y áreas de figuras planas no poligonales utilizando coordenadas rectangulares.
En general este tema incluye las siguientes habilidades específicas:
14. Calcular perímetro y áreas de polígonos no regulares utilizando un sistema de coordenadas rectangulares (MEP, 2012, p. 389).
26. Estimar perímetros y áreas de figuras planas no poligonales utilizando un sistema de coordenadas rectangulares (MEP, 2012, p. 391).
A través de la resolución del problema, el estudiante recurre a utilizar conocimientos previos como el área del rectángulo y trapecio.
El estudiante a través de la resolución emplea la segunda habilidad específica citada previamente, debido a que requiere transformar la imagen del jardín, la cual es irregular y amorfa, en figuras conocidas para poder aproximar el área.
Indicaciones metodológicas
Respecto a la organización de la lecciones, el MEP (2012, p. 41-44) establece dos etapas, el problema Zacate para el jardín puede ser empleado en la II Etapa: La movilización y aplicación de los conocimientos, debido a que los estudiantes están en la capacidad de usar la estrategia de aproximación mediante áreas de figuras planas conocidas desde la primaria, en 5º año se encuentra la habilidad específica:
4. Calcular perímetros y áreas de figuras planas compuestas por triángulos, cuadrados, rectángulos, paralelogramos y trapecios (MEP, 2012, p. 205).
Por tanto, este problema no debe representar una novedad. Sin embargo, queda a criterio del docente, de acuerdo con las características de sus estudiantes, valorar si es pertinente emplearlo para la I Etapa.
De acuerdo con la MEP (2012, p. 400) se deben tener los siguiente aspectos en consideración:
-
El estudio de las áreas puede ser abordado mediante la Historia. Por ejemplo, Arquímedes de Siracusa aproximó el valor del número π . Para ello dibujó un polígono regular inscrito y otro circunscrito a una misma circunferencia, de manera que la longitud de la circunferencia y el área del círculo quedan acotadas por esos mismos valores de las longitudes y las áreas de los dos polígonos. A medida que se incrementa el número de lados del polígono la diferencia se acorta y se obtiene una aproximación más exacta. Partiendo de polígonos de 96 lados cada uno, Arquímedes calculó que el valor de π debía encontrarse entre 3 y 10 ⁄ 71 (aproximadamente 3,1408) o 3 y 1/7 (aproximadamente 3,1429), lo cual es consistente con el valor real de π.
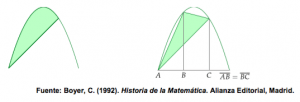
A esta técnica se le conoce con el nombre de método de exhaución. También, demostró que el área del segmento parabólico de la figura que aparece abajo a la izquierda es igual a 4/3 de la del triángulo inscrito de la figura de abajo a la derecha.
Nivel de complejidad y procesos matemáticos
El nivel de complejidad del problema Zacate para el jardín es de Reproducción, esto se asocia con la solución presentada y la intervención de los procesos matemáticos que se describen a continuación:
Razonar y Argumentar:
Este proceso presenta un grado intermedio de participación, debido a que la información matemática está dada en el enunciado, pero no de manera explícita, los estudiantes deben usar e interpretar la escala para determinar las longitudes de los lados de las figuras planas con las que se intenta aproximar el área del jardín. Además, la respuesta que se debe dar se obtiene mediante la suma de diferentes áreas.
Plantear y resolver problemas:
El problema se puede considerar familiar para el estudiante. Además, requiere de emplear fórmulas conocidas, en este caso trapecio y triángulo o rectángulo por tanto, la intervención de este proceso en un grado de participación bajo.
Conectar:
En la solución los estudiantes deben conectar oportunamente la información que les proporciona el contexto del problema, con el cálculo de áreas de figuras planas seleccionadas por el estudiante para aproximar la cantidad de zacate necesaria. Esta es una situación que resulta familiar y similar a las estudiadas previamente. En este sentido la intervención del proceso se puede catalogar como baja.
Comunicar:
En primer lugar los estudiantes requieren solo identificar e interpretar las expresiones matemáticas presentes en el problema, que corresponden a las longitud del jardín "4m de ancho por 5m de largo". Posteriormente, solo deben indicar una respuesta muy puntual. Todo esto implica un grado de intervención bajo del proceso de comunicación.
Representar:
La intervención del proceso es baja, debido a que la información solo deben interpretar los datos que están presentes en el enunciado "4m de ancho por 5m de largo", pero esto es algo que se ha trabajado desde la primaria. Posteriormente, unicamente deden usar los valores que se requieren en la fórmula del área del triángulo, trapecio o rectángulo, que aunque es una representación algebraica, han sido de uso frecuente durante la primaria y secundaria.
Por tanto, cuatro de los procesos matemáticos alcancan una intervención baja, se debe señalar que únicamente Razonar y argumentar alcanzó una intervención intermedia. El nivel de complejidad del problema es de Reproducción, debido a las exigencias cognitivas que implica para el estudiante y que fueron detalladas previamente. Se puede profundizar en la estrategia para determinar los niveles de complejidad en Ruiz (2018). Además puede acceder a los videos de la colección Valoración de Tareas Matemáticas para ampliar los contenidos.